内容:线性代数的应用,包含(计算机图形学,算法,密码学的相关内容)
前置基础:矩阵乘法
算术,代数,算法 | arithmetic, algebra, algorithm¶
先简单的引入一下,从小学的 算术 到中学的 代数 这两者之间的差别。
- 小学的算术
- \((3 + 7) \times 5= 10\times5\)
- \(753+672=1300+120+5=1425\)
- 中学的代数
- \(x^2-2x-3=0\to x\in\{-1,3\}\)
为什么算术比代数简单?¶
-
算术运算的结果是确定的——会变越来越简单。
-
代数运算是没有办法去定义“好”运算的。
- \(x^2-2x-3=x^2-2x+1-4\)
什么是算法¶
算法是一种自动工作的流程,按照小步工作进行自动运算。 比如下面这道题目。 题目: Problem - B - Codeforces
这是 Codeforces 周赛 div2 的一道题目,比较简单,大家可以简单的思考一下
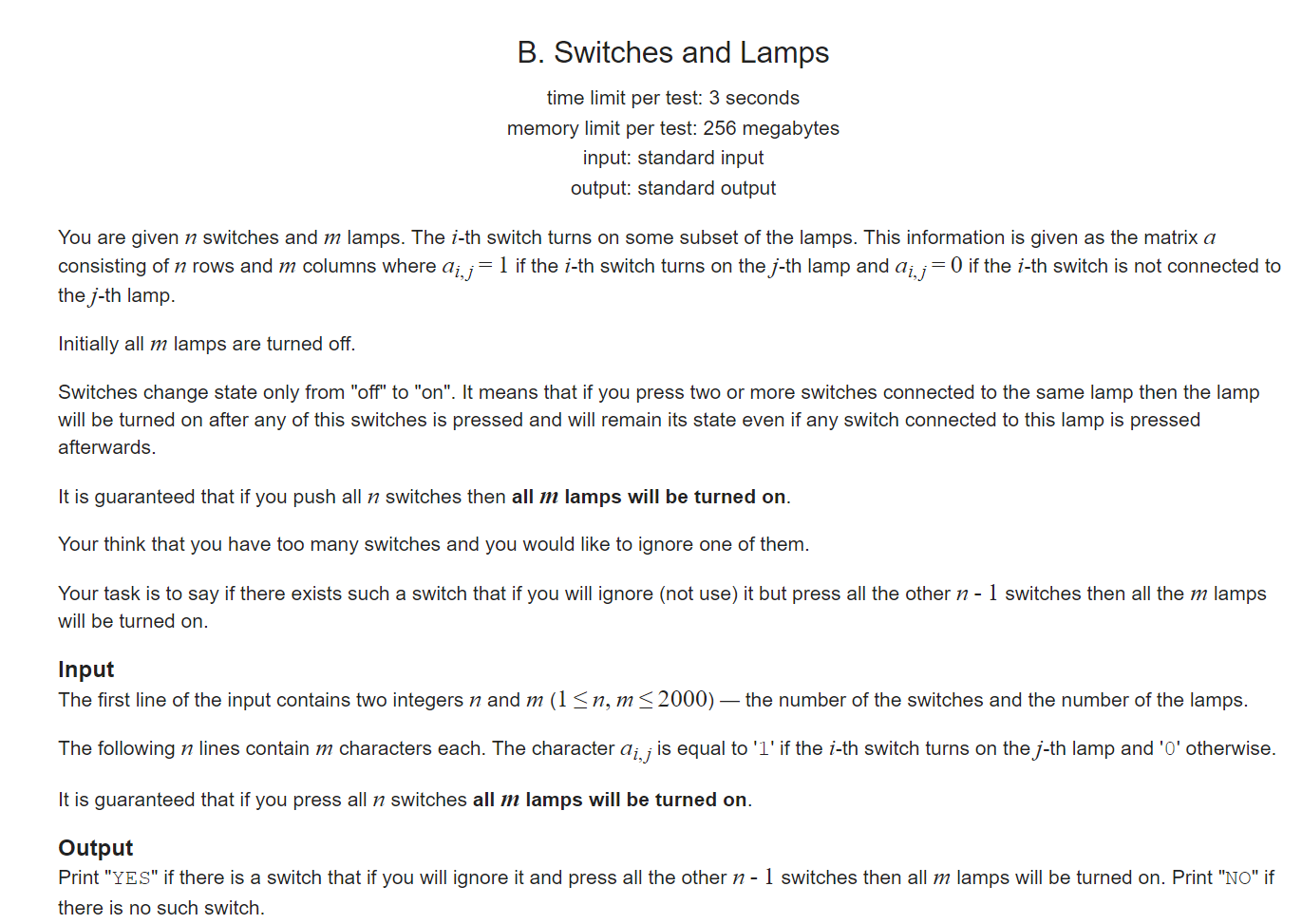
英文看着很长,实际题目很简单,有 n 个开关和 m 盏灯,只要存在一个控制这个灯是开着的这个等就会被点亮。
然后给你 01 矩阵,表示 n 个开关控制 m 盏灯,行列为 1 表示可以让灯亮着,问你能否删掉一个开关,使得所有灯被点亮。
思路想到的很简单,对于每一行求和,如果对于每一行,如果去掉某一行后这一列的和变成 0 ,说明有灯不能删掉,一个简单的枚举法,每一次检测开关的时间复杂度是 \(O(mn)\),所以总的时间复杂度是\(O(mn^2)\),刚好够 \(3s\) 的时间限制。当然,可以用前缀和或者位运算的奇技淫巧进行复杂度降低,这里不进行展开。
那么这个思路从线性代数的角度怎么看呢……
就是求线性无关组,如果在线性无关组里面就是 NO,如果不在线性无关组里面就是 YES,当然线性无关组在这里是唯一的。
线性无关组代表没有冗余的信息,这些信息都是线性无关的,也就是向量之间无法用彼此之间相互表达的含义,因此,在题目里,就是检测有没有开关是冗余的。
源码实现可以参考
Python numpy里面的matrix_rank函数实现。在 \(linalg/\_linalg.py\) 目录下的 \(1973\) 行
这是线性代数的思想在算法竞赛里的一个简单应用。
线性算术 | Linear Arithmetic¶
略过基础性的向量加减运算,我们先重新复习一下数乘。 $$ 2 \times\begin{bmatrix}1\\2\end{bmatrix} = \begin{bmatrix}2\\4\end{bmatrix} $$ 什么意思,这是一个几何上的伸缩运算,把原来的向量拉伸了 \(2\) 倍,由此引到我们线性变换的内容。
线性变换 | Linear Transformation¶

线性代数的一些应用¶
计算机图形学 | Computer Graphics¶
点乘的作用¶
由于不想画图了,所以虚空地讲一下。 点乘在计算机图形学领域主要用于求解两个向量之间的角度。可以想一想这个角度有什么用。
向量是一个即有大小又有方向的量,但是计算机内部是没有方向的这个概念的,所以用一个可以量化的角度去表示向量之间的方向。
叉乘的作用¶
这里不复习相关的定义问题,但是有一些基本的常识性概念。 $$ \vec x \times \vec y = \vec z \quad \vec y \times \vec x = -\vec z $$ 这有什么作用呢,比如在渲染的时候我可以画一个三角形,然后用向量的叉乘快速判断这个点是不是在三角形内部。(可以扩展到任意凸包,求凸包的相关算法可以用点乘,详情参询https://oi-wiki.org/geometry/convex-hull/)
这里我们计算叉乘通常使用右手系,但是在 UE4 和 OpenGL 中使用的是左手系,问题不大,翻转一下就可以了。 向量的叉乘和向量的点乘都可以写成矩阵乘法的形式,可以思考一下怎么个一回事。(提示:伴随矩阵)
真正的变换专场¶
缩放变换¶
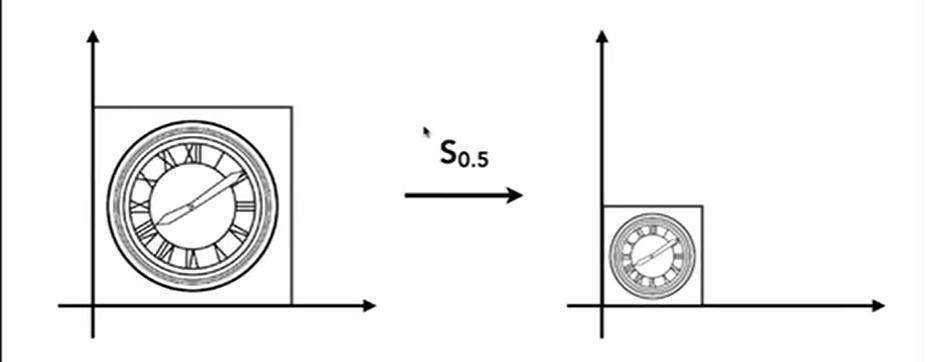
横轴和纵轴都变成了原来的 \(\frac{1}{2}\) 用数学的语言表达呢如下 $$ x^{'} = sx \quad y^{'} = sy $$ 作为一个学过线性代数的人呢,需要学会把这个转换成为矩阵形式,就比如这个样子 $$ \begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}s & 0\\0&s\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix} $$
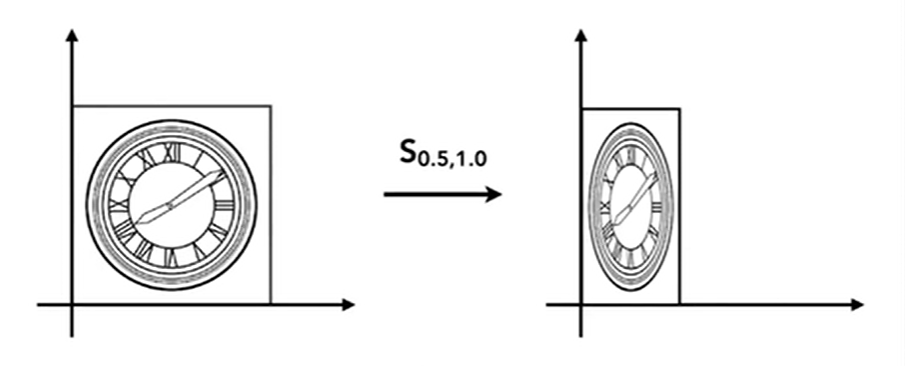
当然,也可以不均匀的缩放,比如 \(x\) 和 \(y\) 一个缩小到 \(\frac{1}{2}\),一个保持不变。 $$ \begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}s_x & 0\\0&s_y\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix} $$
对称变换¶
学过近世代数的同学应该都知道,矩阵运算时非常符合群这个东西的定义的,但是如果从高中数学推导过来呢,群一开始诞生就是为了描述对称性这个东西的。所以矩阵应该是很轻松的就能把对称这个东西给描述出来的。
提示:可以看成是缩放的特殊情况。
切变换 | Sheer¶
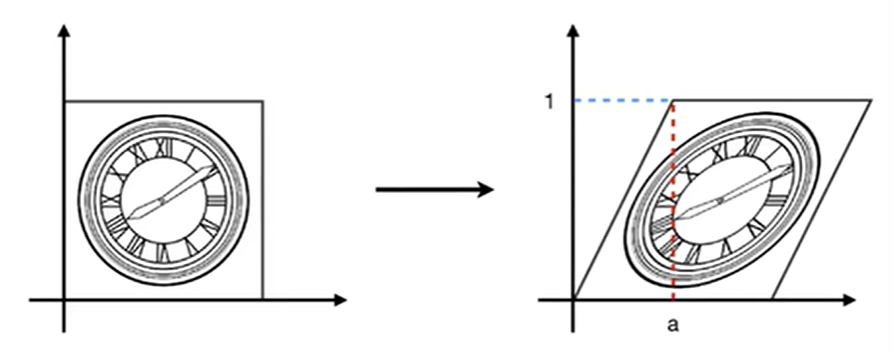 $$
\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}1 & a\\0&1\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
$$
$$
\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}1 & a\\0&1\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}
$$
旋转变换¶
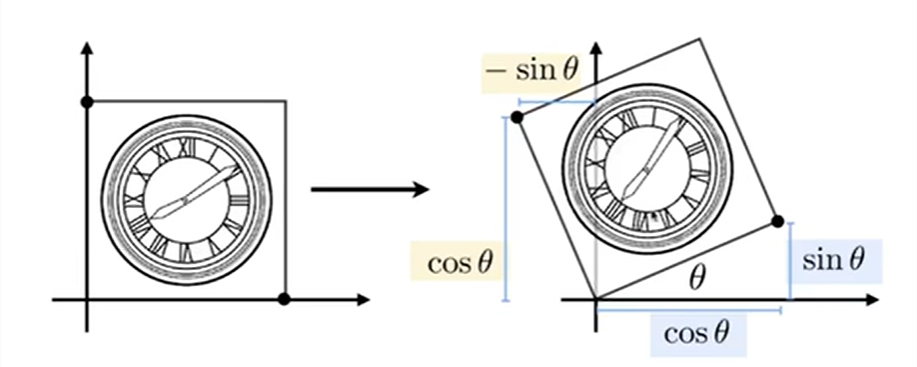 $$
R_\theta = \begin{bmatrix}\cos \theta & -\sin\theta\\sin\theta&\cos\theta\end{bmatrix}
$$
$$
R_\theta = \begin{bmatrix}\cos \theta & -\sin\theta\\sin\theta&\cos\theta\end{bmatrix}
$$
进行一些小总结¶
可以发现上述所有变换都可以写成形如 \(\(x^{'}=ax+by\quad y^{'}=cx+dy\)\) 转换成为矩阵形式也就是 $$ \begin{bmatrix}x^{'}\\y^{'}\end{bmatrix} = \begin{bmatrix}a & b\\c&d\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix} $$
平移¶
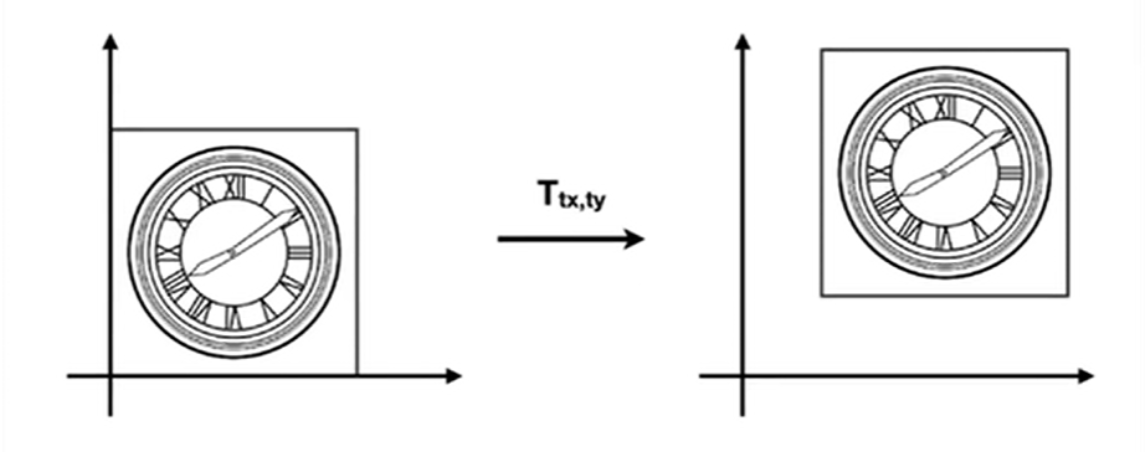 可以想一想还能不能愉快的写成一个矩阵左乘的形式了?我简洁的矩阵形式怎么没有了?
只能写成如下形式:
$$
\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix} = \begin{bmatrix}a & b\\c&d\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}+\begin{bmatrix}t_x\\t_y\end{bmatrix}
$$
好像很简单,但是这形式和之前的不统一。也表明平移不是一个很正经的线性变换。这种不统一的形式也不适合程序员偷懒,凭啥同样是二维变换,平移就要搞特殊?
可以想一想还能不能愉快的写成一个矩阵左乘的形式了?我简洁的矩阵形式怎么没有了?
只能写成如下形式:
$$
\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix} = \begin{bmatrix}a & b\\c&d\end{bmatrix}\begin{bmatrix}x\ y\end{bmatrix}+\begin{bmatrix}t_x\\t_y\end{bmatrix}
$$
好像很简单,但是这形式和之前的不统一。也表明平移不是一个很正经的线性变换。这种不统一的形式也不适合程序员偷懒,凭啥同样是二维变换,平移就要搞特殊?
答案是有统一形式的,但是代价是什么呢?计算机科学中时间复杂度和空间复杂度更多情况下是不能同时兼得的。
这次答案很简单,就是把原先的 \(2\times2\) 的矩阵升维,变成 \(3\times3\) 的矩阵,用更多的计算时间和存储空间换取一个更加统一的计算形式。
首先先讲一下矩阵升维之后,我们对原来二维的点和向量做了些什么。 点 \(dot = (x,\ y,\ 1)^{T}\) 向量 \(vec = (x,\ y,\ 0)^{T}\) 1和0在这里起到了一个表示身份的作用,同时,向量具有向量不变性,因此末尾为 0 - 向量 + 向量 = 向量 - 向量 - 向量 = 向量 - 点 - 点 = 向量 - 点 + 向量 = 点 - 点 + 点 = ?(根据某种扩充定义,表示两个点的中点)
扩充定义如下:\((x,\ y,\ w)^T\) 是表示二维的点\((x/w,\ y/w,\ 1)^T\)
因此统一形式如下 $$ \begin{bmatrix}x^{'}\\y^{'}\\1\end{bmatrix} = \begin{bmatrix}a & b & t_x\\c&d&t_y\\0&0&1\end{bmatrix}\begin{bmatrix}x\ y\\1\end{bmatrix} $$ 希望写到这里能更好的帮你理解很多教科书上突然冒出的 四元数 这个奇妙的概念,因为那是在三维空间中,额外升了一维。(01作业光栅化展示)
但是这远远不是图形学,他只是入门,甚至门都没有入。更深一点的比如摄像头的旋转,视图的变换都没有讲到,这些依旧属于矩阵变换的范畴,6个自由度导致矩阵越来越难写,所以对线性代数的功底提出了很高的要求。
光栅化,光线追踪,辐射度量学,基于物理的渲染,以及到最后进行游戏引擎的开发,需要数据结构,需要算法,需要为了更逼真的图片去榨干GPU的性能。这都是图形学。
中国科技大学有一套属于自己的图形学Lab,西安交通大学在2024年也在逐步开发自己的图形学作业代码框架,上海交通大学和浙江大学会在本科阶段讲一点蒙特卡洛渲染的内容,正视自己与其他学校本科生之间的差距,努力进步。
图形学是概率论,微积分,线性代数,物理学都需要的一门学科,反正感觉挺好玩的,比如蒙特卡洛积分。
talk is cheap, show me the code
算法¶
矩阵快速幂¶
快速幂¶
求 \(a^b\ mod\ c\) 的问题。 很多人会觉得这很简单,但是如果 \(b\) 很大呢? $$ a^{2b} = (a^2)^b \quad a^{2b+1} = a\times (a^2)^b $$ 如此不断的二分下去就可以得到答案,用到的也是二分的思想。 举个例子吧,毕竟上面的算式还是太抽象了 $$ a^{13} = a^{(1101)_2} = a^8 · a^4·a^1 $$ 这样我们只需要知道 \(a^1,a^2,...a^{2^n}\) 就可以快速的算出 \(a^{2^{n+1}}\) 的幂次。只需要将对应二进制位为 1 的整系数幂乘起来就行了,代码如下:
long long quick_pow(long long a, long long b)
{
long long res = 1;
while (b > 0) {
if (b & 1) res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
矩阵乘法¶
懒得讲,线代应该还没忘。
真正的矩阵快速幂¶
矩阵快速幂,顾名思义,就是 矩阵乘法 + 快速幂。好的我讲完了(不是)
但是很多人接触矩阵快速幂应该是在计算斐波那契数列那边接触到的,然而并没有进行一个深入。
斐波那契数列¶
但是还是先温习一下斐波那契数列怎么用矩阵加速求的,刚才计算机图形学的东西希望还没有忘干净 $$ \begin{bmatrix}F_{n-1} & F_{n-2}\end{bmatrix}\begin{bmatrix}1&1\\1&0\end{bmatrix} = \begin{bmatrix}F_{n} & F_{n-1}\end{bmatrix} $$
定义初始矩阵 \(\text{ans} = \begin{bmatrix}F_2 & F_1\end{bmatrix} = \begin{bmatrix}1 & 1\end{bmatrix}, \text{base} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}。\)
那么,\(F_n 就等于 \text{ans} \text{base}^{n-2}\) 这个矩阵的第一行第一列元素,也就是 \(\begin{bmatrix}1 & 1\end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^{n-2}\)的第一行第一列元素。
const int mod = 1000000007;
struct Matrix {
int a[3][3];
Matrix() { memset(a, 0, sizeof a); }
Matrix operator*(const Matrix &b) const {
Matrix res;
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 2; ++j)
for (int k = 1; k <= 2; ++k)
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
return res;
}
} ans, base;
void init() {
base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;
ans.a[1][1] = ans.a[1][2] = 1;
}
void qpow(int b) {
while (b) {
if (b & 1) ans = ans * base;
base = base * base;
b >>= 1;
}
}
int main() {
int n = read();
if (n <= 2) return puts("1"), 0;
init();
qpow(n - 2);
println(ans.a[1][1] % mod);
}
HDU 1005 Number Sequence¶
\(\text{给出一个数列定义如下:}f(1)=1,f(2)=1,f(n)=Af(n-1)+Bf(n-2),\text{计算}f(n)\) $$ \begin{bmatrix}F(n-1) \ F(n-2)\end{bmatrix}\begin{bmatrix}A&B\\1&0\end{bmatrix} = \begin{bmatrix}F(n) \ F_(n-1)\end{bmatrix} $$
LightOJ 1070 Algebraic Problem¶
给出 \(a+b\) 和 \(ab\) 的值,求\(a^n+b^n\) 答案对 \(2^{64}\) 取模
先说模数,这个模数很好,直接开 unsigned long long 自然溢出就可以了。虽然可能不安全
$$
(a^n+b^n)(a+b)=(a^{n+1}+b^{n+1}+ab(a^{n-1}+b^{n-1}))
$$
于是,令 \(A =a+b,B=ab,F(n) =a^n+b^n\),有
$$
\begin{bmatrix}A&-B\\1&0\end{bmatrix}\begin{bmatrix}F(n) \ F(n-1)\end{bmatrix} = \begin{bmatrix}F(n+1) \ F_(n)\end{bmatrix}
$$
所以这也是一种迭代的思想(牛顿迭代法算根号)
矩阵快速幂可以用来加速动态规划,还有广义的矩阵乘法以及转移矩阵的相关操作,但是这里不想涉及,因为有点超纲了,有的还是控制论那边的内容。
搜索引擎¶
特征向量¶
实际上,特征向量还能用来求解微分方程,因为积分和微分都是线性运算,但是这里就不展开了。
价值 $25,000,000,000的特征向量¶
Google 成功的秘诀:为互联网上所有的页面重要性排序
- Google 每天都爬取整个互联网上的数据,并且建立页面的索引和链接关系,并计算所有网页的排序
- Page Rank: 在网页上的 random walk
- 在每个网页都随机点击链接
- \(Ax = x\) 就是稳定的 “概率分布” (\(A^{\infty}\) 恰好是它的解,maybe有点类似信息论里的马尔科夫信源) $$ A= \begin{bmatrix}0&0&1& \frac{1}{2} \\ \frac{1}{3}&0&0&0 \\ \frac{1}{3}&\frac{1}{2}&0&\frac{1}{2} \\ \frac{1}{3}&\frac{1}{2}&0&0\end{bmatrix} x=\begin{bmatrix}0.387\\0.129\\0.290\\0.194\end{bmatrix} $$
推荐系统¶
推荐系统:如何为你预测对商品的评分?
| Alice | Bob | Cathy | Davy | |
|---|---|---|---|---|
| 苹果 | 1 | ? | 1 | ? |
| 橙子 | ? | ? | ? | 3 |
| 香蕉 | 3 | ? | ? | ? |
| 西瓜 | 5 | 4 | ? | ? |
矩阵分解:\(M_{m\times n}=P_{m\times k}\times Q_{k\times {n}}\) \(k\) 是隐藏的 “维度” (Latent factor model) - 如果 \(k\) 很小,我们就有足够的数据求解出 “最合适” 的 \(P\) 和 \(Q\) - 每个人对物品的偏好是一系列特征的线性组合
密码学 | Crypto¶
今天的密码学内容是格密码的专场,是密码学的一些前沿研究内容了,属于现代密码学再往后的后量子时代密码学的内容,整点现代的,但是无加解密相关的内容,只关心什么是格,因此是堂堂正正的数学课。 古典的密码没啥好玩的,现在题目出的和考脑洞是一样的,只有完整的逆向了出题人的脑洞才能做出来。(某种程度上的逆向) 现代密码学模块的话,算法的实现必不可少,但是要整点现代的话应该是安全证明那边。
先介绍一下格密码的成就(?) 已经公布的4个NIST抗量子标准优胜算法中,有3个是格密码,占比达到了惊人的75%,遥遥领先于其他算法。(截止到2022年9月)
在 7 个正式入选第三轮的算法中,有5个都属于格密码的范畴,而与此同时,在我国2019年密码学会举办的后量子密码算法竞赛中,格密码也在其中占据了相当大的比例。
 近代格密码的时间线
近代格密码的时间线
- 1982:LLL basis reduction theorem
- 使用Lattice来做Cryptanalysis
- 1996:Ajtai-Dwork
- 第一次把Lattice中Average-case与Worst-case的复杂度问题关联起来
- 提出了使用Lattice构造的One-way Function与CRHF(Collision Resistant Hash Function)
- 2002:找到了Average-case/worst-case复杂度之间的关系,基于Lattice的协议变得更加高效
- 2005:Regev提出了LWE,并且发现其量子抵抗性
- 提出PKE,IBE,ABE,FHE等等的可能性
格 | Lattice¶
Lattice是什么?¶
Lattice可以被想象成是一个空间中很多有规律分布的、离散的点。 \(n\)维空间中最简单的 Lattice 就是 Integer Lattice(整数格)。整数格中最简单的就是基于笛卡尔坐标系的\(i,j\)...等基向量组成的空间。
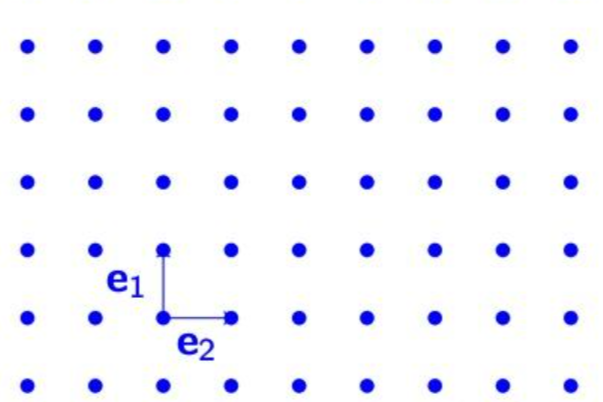
Lattice与Bases(格与基)¶
更好的描述一个格的方法是使用基向量。
我们假设一个格拥有基向量\(b_1,b_2...b_n\)。那么这个Lattice就是它的基向量的任意线性组合的集合,我们也可以把所有基向量组合成矩阵 \(B\) 来表示。 注意,一个格可以有多个基底,不是一一对应的关系。 如果系统性的定义一下Lattice的话,那么我们可以说Lattice是 \(R^n\) 这个空间中的一个离散的、具有加法运算的子群(A discrete additive subgroup)。
Lattice 的基本属性¶
我们知道,在一个线性空间里面,一个空间 \(V\) 的 Determinant(行列式)\(det(V)\) 代表了这个空间所有的基向量 \(b_i\) 所组成的几何体的体积。在二维空间里,两个基向量 \(b_1,b_2\) 组成的平行四边形的面积就是这个空间的行列式。
同理可得,一个Lattice的行列式也是一样的——对应的基向量所组成的平行六面体的体积。
Lattice 的密度¶
我们可以用一个Lattice的Determinant来衡量这个格的点阵分布的密度。
首先,我们把上一部分基向量组成的多面体的中心挪到原点上来。这样,空间 \(P\) 仍然保持相同的体积。
随后,我们可以把这个多面体复制多份,然后平移到每一个Lattice中的点上。这样我们就会得到很多份 \(P\),并且这些多面体可以平分整个多维空间 \(R^n\)。
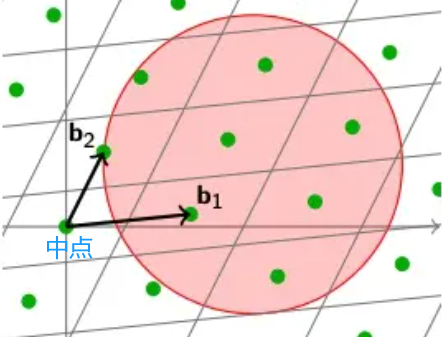
此时,我们如果在这个空间中任意的画一个球体(多维空间即超球体),然后可以数数看这个球体中覆盖了多少Lattice里的点。点的数量平均于球体的体积,就是这个格的密度了。
最短距离¶
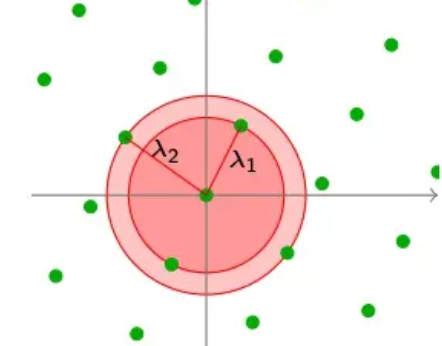
我们一般用 \(\lambda_1\) 来定义整个格中点与点之间最短的距离。一般为了方便理解,我们就把其中的一个点设置成坐标轴 \(O\) 点,然后 \(\lambda_1\)就变成了距离 \(O\) 点距离最近的格点。
距离函数与覆盖半径¶
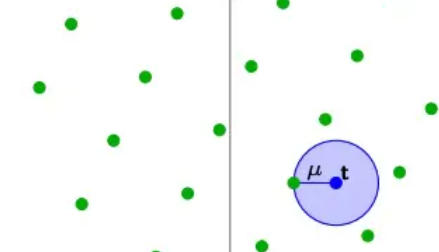
给定任意一个点 \(t\)(这个点不需要在Lattice上),我们可以定义距离函数 \(\mu(t,L)\) 为这个点到附近的Lattice点的最短距离。
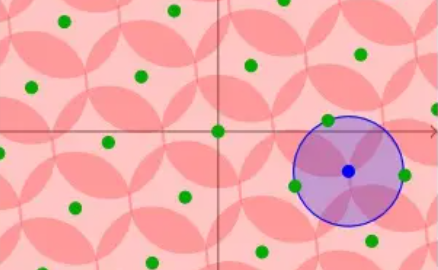
同理可得,我们也可以左右移动 \(t\) 的位置,然后就可以找到在这个 Lattice 中可以得到的最大的 \(\mu\)。我们一般称这个最大值叫覆盖半径(Covering Radius)。 直到所有的圆正好完美的覆盖了所有的空间的时候,这个时候的半径,就是我们之前得到的 \(\mu\) 了。这就是覆盖半径这一名字的由来。
Minkowski凸集定理¶
最重要的用处就是给出一个Lattice中最短向量的一个上限值。理解这个玩意可能需要引入凸包的概念,就给结论吧。
SVP问题(Shortest Vector Problem)¶
顾名思义,最短向量问题(SVP,Shortest Vector Problem) 就是在格中找到“长度”最短的向量。 一个很直观的想法,如果我们手上的格基是相互正交的,那么我们只需要遍历格基中的各个向量就可以找到最短的向量了。
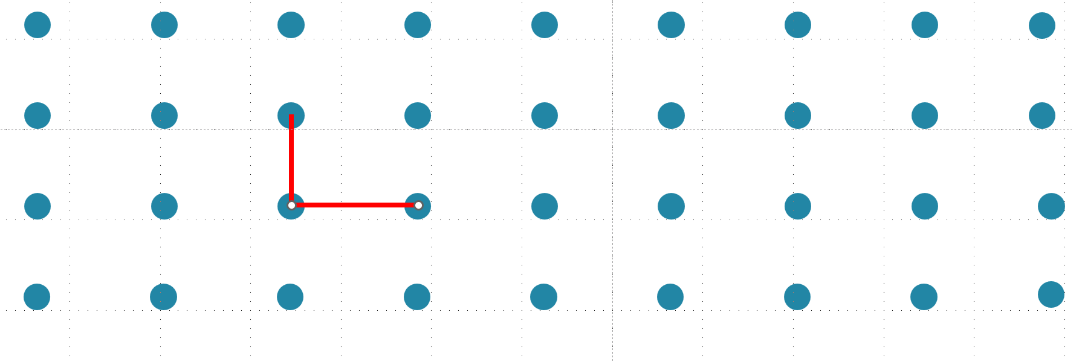
于是我们就发现了这个惊天秘密:为了找到最短向量,就要尽量使得格基正交。
CVP问题(Closest Vector Problem)¶
Lattice中另一大问题就是最近向量问题(CVP,Closest Vector Problem)了。问题的定义是这样的:给定连续空间中任意的一个点 \(t\) ,找到距离这个点最近的格点 \(B_x\)
CVP → SVP¶
如果能够一招鲜吃遍天,那何乐而不为呢?另外就是因为日益增长的攻击手法和不太够的脑容量之间的矛盾。 为了方便演示,假设我们有一个一维的格,然后我们需要找到距离点 \(t\) 最近的格点 \(B_x\)

那么我们可以进行一个类似于“升维”的操作,使得 \(t\) 点也成为新格的一个格点。
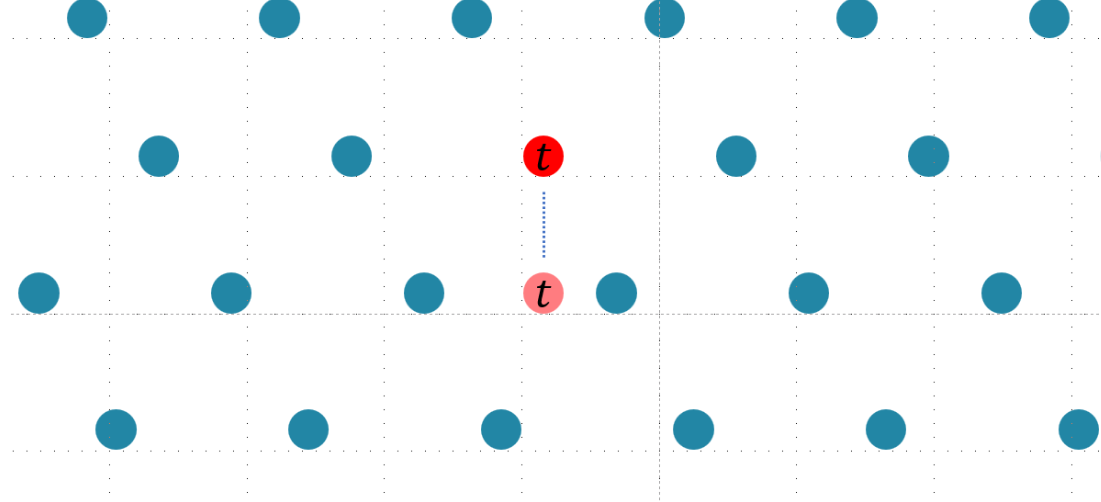
然后在这个新格中我们解决一下 SVP,找到最短向量,然后再将这个最短向量投影回原来的低维中,我们就能找到原来格中距离 \(t\) 最近的格点 \(B_x\) 了。 于是压力来到解决 SVP 这边,而我们之前也说了,“为了找到最短向量,就要尽量使得格基正交”,于是压力又来到 找到正交基 这边。(施密特正交化用在哪里有点数了哈)
LLL 算法¶
没错,用来寻找正交基的算法,大概也许可能,很多人只要会掉包就可以了。
Fear the science. 尽管很前沿,但是还是那句话:这些都是入门,甚至入门的边都算不上,敬畏科学。
线性规划¶
软件工程有一门课叫凸优化,但是我作为一个网安的没学过也不会学(理直气壮)
图论¶
二分图,网络流啥的,由于算法竞赛退役多年,人菜,留待后人补充。(相信后人的智慧)
参考 | Reference¶
南大蒋炎岩老师对中学生JSNOI分享: https://jyywiki.cn/OI/
闫令琪老师的Games101: https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
3blue1brown: https://www.3blue1brown.com/
Zach数学系列: https://www.youtube.com/watch?v=i8FukKfMKCI&t=110s
Van1sh的博客:http://jayxv.github.io/2023/10/17/密码学基础之格中难题与格基规约/
Steven Yue的文章: Steven Yue - 知乎 (zhihu.com)
2020年Simons格密码讲座:Lattices: Algorithms, Complexity, and Cryptography Boot Camp (berkeley.edu)
